LeNet5.ipynb
Let's talk about how we can express models in PyTorch
import torch # for all things PyTorch
import torch.nn as nn # for torch.nn.Module, the parent object for PyTorch models
import torch.nn.functional as F # for the activation function
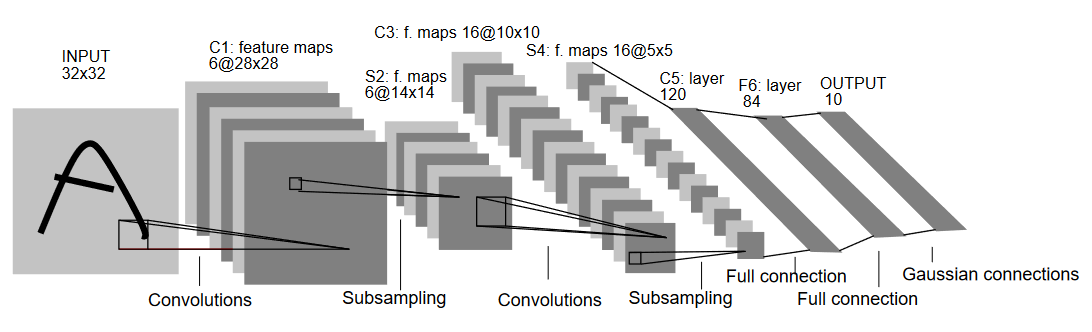
Figure: LeNet-5
Above is a diagram of LeNet-5, one of the earliest convolutional neural nets, and one of the drivers of the explosion in Deep Learning. It was built to read small images of handwritten numbers (the MNIST dataset), and correctly classify which digit was represented in the image.
Here's the abridged version of how it works:
- Layer C1 is a convolutional layer, meaning that it scans the input image for features it learned during training. It outputs a map of where it saw each of its learned features in the image. This "activation map" is downsampled in layer S2.
- Layer C3 is another convolutional layer, this time scanning C1's activation map for combinations of features. It also puts out an activation map describing the spatial locations of these feature combinations, which is downsampled in layer S4.
- Finally, the fully-connected layers at the end, F5, F6, and OUTPUT, are a classifier that takes the final activation map, and classifies it into one of ten bins representing the 10 digits.
How do we express this simple neural network in code?
class LeNet(nn.Module):
def __init__(self): # Constructor method to initialize the LeNet model
super(LeNet, self).__init__() # Call parent class (nn.Module) constructor
# 1 input image channel (black & white), 6 output channels, 3x3 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 3) # First convolutional layer: 1 input channel, 6 output channels, 3x3 kernel
self.conv2 = nn.Conv2d(6, 16, 3) # Second convolutional layer: 6 input channels, 16 output channels, 3x3 kernel
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 6 * 6, 120) # First fully connected layer: 576 inputs (16*6*6), 120 outputs
self.fc2 = nn.Linear(120, 84) # Second fully connected layer: 120 inputs, 84 outputs
self.fc3 = nn.Linear(84, 10) # Output layer: 84 inputs, 10 outputs (for 10 classes)
def forward(self, x): # Forward pass method that defines how data flows through the network
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2)) # Apply first conv layer, ReLU activation, then 2x2 max pooling
# If the size is a square you can only specify a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2) # Apply second conv layer, ReLU activation, then 2x2 max pooling
x = x.view(-1, self.num_flat_features(x)) # Flatten the tensor for fully connected layers
x = F.relu(self.fc1(x)) # Apply first fully connected layer with ReLU activation
x = F.relu(self.fc2(x)) # Apply second fully connected layer with ReLU activation
x = self.fc3(x) # Apply final output layer (no activation for raw logits)
return x # Return the final output tensor
def num_flat_features(self, x):
size = x.size()[1:] # all dimensions except the batch dimension
num_features = 1
for s in size:
num_features *= s
return num_features
Looking over this code, you should be able to spot some structural similarities with the diagram above.
This demonstrates the structure of a typical PyTorch model:
- It inherits from
torch.nn.Module- modules may be nested - in fact, even theConv2dandLinearlayer classes inherit fromtorch.nn.Module. - A model will have an
__init__()function, where it instantiates its layers, and loads any data artifacts it might need (e.g., an NLP model might load a vocabulary). - A model will have a
forward()function. This is where the actual computation happens: An input is passed through the network layers and various functions to generate an output. - Other than that, you can build out your model class like any other Python class, adding whatever properties and methods you need to support your model's computation.
Let's instantiate this object and run a sample input through it.
net = LeNet()
print(net) # what does the object tell us about itself?
input = torch.rand(1, 1, 32, 32) # stand-in for a 32x32 black & white image
print('\nImage batch shape:')
print(input.shape)
output = net(input) # we don't call forward() directly, PyTorch's nn.Module class automatically calls the appropriate method on the input object. Makes sure there is proper gradient tracking, etc.
print('\nRaw output:')
print(output)
print(output.shape)
LeNet( (conv1): Conv2d(1, 6, kernel_size=(3, 3), stride=(1, 1)) (conv2): Conv2d(6, 16, kernel_size=(3, 3), stride=(1, 1)) (fc1): Linear(in_features=576, out_features=120, bias=True) (fc2): Linear(in_features=120, out_features=84, bias=True) (fc3): Linear(in_features=84, out_features=10, bias=True) )
Image batch shape: torch.Size([1, 1, 32, 32])
Raw output: tensor([[-0.0128, 0.0029, -0.0521, -0.0098, -0.0484, -0.1122, -0.0994, 0.0443, -0.0036, -0.0492]], grad_fn=AddmmBackward) torch.Size([1, 10])
There are a few important things happening above:
First, we instantiate the LeNet class, and we print the net object. A subclass of torch.nn.Module will report the layers it has created and their shapes and parameters. This can provide a handy overview of a model if you want to get the gist of its processing.
Below that, we create a dummy input representing a 32x32 image with 1 color channel. Normally, you would load an image tile and convert it to a tensor of this shape.
You may have noticed an extra dimension to our tensor - the batch dimension. PyTorch models assume they are working on batches of data - for example, a batch of 16 of our image tiles would have the shape (16, 1, 32, 32). Since we're only using one image, we create a batch of 1 with shape (1, 1, 32, 32).
We ask the model for an inference by calling it like a function: net(input). The output of this call represents the model's confidence that the input represents a particular digit. (Since this instance of the model hasn't learned anything yet, we shouldn't expect to see any signal in the output.) Looking at the shape of output, we can see that it also has a batch dimension, the size of which should always match the input batch dimension. If we had passed in an input batch of 16 instances, output would have a shape of (16, 10).